Daniel Ellsberg, exanalista de las Fuerzas Armadas de Estados Unidos, demostró por qué tenemos aversión a la ambigüedad y preferimos los riesgos cuantificables a aquellos que no se pueden determinar, resaltando la distinción establecida por Knight entre riesgo e incertidumbre. Esta aportación fundamental a la teoría de la decisión, la demostró en 1961, y se conoce con el nombre de paradoja de Ellsberg. Veámosla.
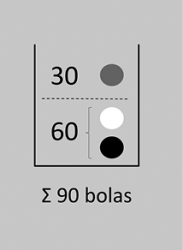
| Figura 11: Composición de la urna de la paradoja de Ellsberg. |
Imaginemos que tenemos una urna con 90 bolas, de las cuales 30 son grises y el resto son blancas y negras, pero desconocemos en qué proporción (véase la figura 11).
Se va a extraer la pri
mera bola. ¿Cuál sería nuestra apuesta, la opción I o la opción II?
- Opción I: apostar que va a salir una bola gris.
- Opción II: apostar que va a salir una bola negra.
Se introduce de nuevo la bola sacada en la urna y se procede a extraer una segunda bola. ¿Con cuál de estas opciones nos parecería mejor ahora?:
- Opción III: apostar que va a salir una bola gris o blanca.
- Opción IV: apostar que va a salir una bola negra o blanca.
Los resultados que obtuvo Ellsberg fueron que la mayoría de las personas elegían la opción I frente a la II, y la IV frente a la III. Esto demuestra nuestra aversión a la ambigüedad, pues si nos fijamos, preferimos las opciones con probabilidades conocidas frente a aquellas cuyas probabilidades se desconocen. Algunos investigadores apuntan que esto depende del hecho de que las probabilidades están ocultas para quien toma la decisión en lugar de ser completamente incognoscibles.
Sabiendo que en la urna hay 90 bolas (30 grises y 60 blancas y negras) se dan las siguientes situaciones:
- Opción I: tenemos ⅓ de probabilidades de ganar.
- Opción II: desconocemos la probabilidad de ganar.
- Opción III: desconocemos la probabilidad de ganar.
- Opción IV: tenemos ⅔ de probabilidades de ganar.
David Morcillo, en su blog Deuda Externa, compara este resultado con el refrán «más vale pájaro en mano que ciento volando». Pero estos resultados no solo los vemos en el laboratorio, también se producen en el mundo real. Morcillo pone como ejemplo el hecho de que las alertas sanitarias nuevas, como la de la gripe A, cuyas consecuencias son difíciles de estimar, provocan mayor preocupación en la sociedad que la típica gripe común, que se declara todos los años pero cuyos efectos son conocidos y pueden ser cuantificados, a pesar de que el año pasado afectó a un mayor número de personas que la gripe A. Este miedo a lo desconocido o, en este caso, a lo no cuantificable hace que prefiramos tomar decisiones en contextos de riesgo, y no de incertidumbre o ambigüedad.
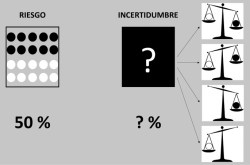
Lo que han hecho otros experimentos, siguiendo la paradoja de Ellsberg, ha sido utilizar dos urnas, una en la que se informa del número de bolas que hay de cada color y otra en la que no se especifica ninguna proporción (véase la figura 12). Indicando previamente el color de la bola, los participantes en el experimento debían elegir la urna con mayor probabilidad de que saliese una bola de dicho color. Los resultados eran similares: la gente evitaba la ambigüedad, aun cuando esa decisión no maximizaba su utilidad.
Figura 12: Otra versión de la paradoja. Esquema utilizado en otros estudios usando la paradoja de Ellsberg. En la urna del riesgo se muestra la distribución de bolas en función de su color, mientras que en la urna de la incertidumbre se desconoce dicha probabilidad. Las posibilidades van desde que todas las bolas sean de un mismo color (blanco o negro), hasta que existan más bolas de un color que de otro, pasando por que la mitad de las bolas sean de un color y la otra mitad, del otro.
Algunos autores sugieren que tendemos a creer que la composición del conjunto de bolas en la urna con incertidumbre no está uniformemente distribuida, y que las distribuciones «desfavorables» (urnas con menos bolas del color que queremos que salga) son más probables. Las personas prefieren apostar por las urnas cuyas probabilidades se conocen (p=0,5 de sacar bola negra y p=0,5 de obtener bola blanca), y no por las urnas con incertidumbre, pues creen que la probabilidad es menor que 0,5 (p<0,5 en el caso de la bola negra y p<0,5 si es bola blanca). Esto es una paradoja, pues en el segundo caso las probabilidades no suman 1. Esto se debe a que en la opción I estamos apostando a que hay más bolas blancas que negras, mientras que en la opción IV apostamos al revés, a que hay más negras que blancas, lo cual es una contradicción, pues las bolas son las mismas.
Pero ¿por qué tendemos a evitar aquellas decisiones que presentan un mayor nivel de incertidumbre? Básicamente por nuestra aversióna las pérdidas. Cuando estas son negativas, el dolor que nos causan es mayor que la alegría que nos provoca una ganancia de similar cuantía, como ya hemos explicado anteriormente. Por este motivo, si vamos a arriesgarnos exigimos que las recompensas sean mayores.
¿Con qué datos contamos cuando decidimos? La información que nos llega no es la misma que la que percibimos. De ahí que la atención sea clave a la hora de decidir. Cuando nos arriesgamos, nuestra decisión se basa en la información que hemos extraído del entorno (cuántas bolas azules y cuántas rojas hay en la urna del riesgo), así como en nuestras actitudes frente al riesgo (si estoy dispuesto a apostar por la urna de la incertidumbre a pesar de no saber la proporción de bolas de cada color que contiene).
Sin embargo, y como comentan en el episodio de Brain Games mencionado, «cada vez que tomamos una decisión arriesgada, en nuestra mente se libra una batalla». Hablan de que una parte de nuestro cerebro está calculando cifras y sopesando probabilidades, mientras que la otra parte, la emocional, es la que a menudo gana la batalla cuando se trata de decidir qué riesgos se corren. Pero ¿qué ocurre realmente en nuestro cerebro cuando tomamos decisiones arriesgadas?