Esta fase ya se ha estudiado referida al análisis de un solo balance. Ahora, lo haremos referido a dos. En la tabla 8-5 se reflejan expresados en porcentajes los dos balances de situación de la tabla 8-4, donde se plasman en valores absolutos.
En los porcentajes anteriores se puede apreciar que, mientras que el activo casi no ha variado de un año a otro, en el patrimonio neto más pasivo se han producido variaciones importantes. Así, el patrimonio neto ha aumentado y, en cambio, han disminuido tanto el pasivo corriente como el no corriente. En definitiva, han disminuido las deudas de la empresa y ha disminuido su riesgo debido al aumento en el patrimonio neto.
Representación gráfica de los balances
La representación gráfica de dos o más balances se hace de la misma forma que se ha estudiado para un solo balance.
En el ejemplo que estamos estudiando, la representación gráfica de los balances será como se muestra en las figuras 8-1 y 8-2.
Figura 8-1: Balances del año 1 en porcentajes
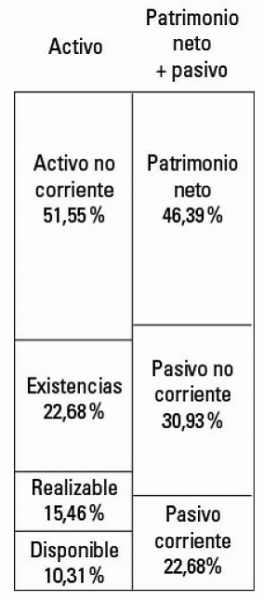
Figura 8-2: Balances del año 2 en porcentajes
Los gráficos de estas dos figuras permiten ver más claramente lo que los porcentajes ya habían permitido detectar
En el análisis dinámico se pueden presentar también las evoluciones del activo y del pasivo por separado, a fin de resaltar de forma más clara las variaciones producidas.
Así, en la figura 8-3 se puede apreciar que la evolución del activo no ha sufrido variaciones importantes: se ha producido un ligero aumento del inmovilizado, tanto las existencias como el disponible disminuyen levemente, y el realizable aumenta ligeramente.
Por su parte, el pasivo (figura 8-4) sí ha sufrido variaciones importantes. La empresa se ha capitalizado a oj os vista, pues el patrimonio neto ha pasado de significar el 40,63% a suponer el 46,39%. Por contra, el pasivo (tanto el corriente como el no corriente) ha disminuido en su conjunto, y muestra un menor volumen de deuda.
Figura 8-3: Evolución comparativa del activo
Figura 8-4: Evolución comparativa del patrimonio neto más el pasivo
El cálculo de porcentajes es una operación matemática fundamental y es utilizado en diversas áreas, desde las finanzas hasta la vida cotidiana:
1. Cálculo del Porcentaje:
La fórmula básica para calcular el porcentaje de un número en relación con otro es:
Porcentaje=(ParteTotal)×100
Donde:
- Parte: Es el valor que deseas expresar como porcentaje.
- Total: Es el valor total del cual la parte es un porcentaje.
Ejemplo:
Si tienes 80 manzanas y 20 de ellas son verdes, el porcentaje de manzanas verdes sería:
Porcentaje de Manzanas Verdes=(2080)×100=25%
2. Cálculo de la Variación Porcentual:
La fórmula para calcular la variación porcentual entre dos valores es:
Variacioˊn Porcentual=(Nuevo Valor−Valor AntiguoValor Antiguo)×100
Ejemplo:
Si una acción se valoriza de $50 a $60, la variación porcentual sería:
Variacioˊn Porcentual=(60−5050)×100=20%
3. Cálculo del Valor Original o Final Después de un Cambio Porcentual:
Para calcular el valor original o final después de un cambio porcentual, puedes usar las siguientes fórmulas:
Valor Original=Valor Final1+(Cambio Porcentual/100)
Valor Final=Valor Original×(1+Cambio Porcentual100)
Ejemplo:
Si tienes un producto con un precio original de $100 y hay un descuento del 20%, el nuevo precio sería:
\text{Nuevo Precio} = \frac{100}{1 + (20/100)} = $83.33
4. Cálculo del Porcentaje de un Número:
Si quieres calcular el porcentaje de un número sin tener un total específico, la fórmula es:
Porcentaje de un Nuˊmero=(NuˊmeroTotal)×100
Ejemplo:
Si has estudiado 3 horas de un total de 5 horas, el porcentaje de tiempo estudiado sería:
Porcentaje de Tiempo Estudiado=(35)×100=60%