El dinero pierde valor a medida que pasa el tiempo, entre otros motivos por la inflación, que hace que los precios de los bienes vayan subiendo. Esto implica que, con la misma cantidad de dinero, cada vez puedan adquirirse menos bienes.
Supongamos que la inflación anual es del 4%, lo que significa que los precios medios de todos los bienes suben una media del 4% al año. Si una empresa tiene 100 euros hoy y los deja en la caja fuerte, dentro de un año podrá comprar el 4% menos de los bienes que podría comprar hoy.
Cálculo del valor futuro de un importe
El valor futuro de una cantidad es la conversión a euros del futuro de unos euros que tenemos hoy. Por lo tanto, el valor futuro se obtiene transformando en euros del futuro un valor actual. Para efectuar la conversión de euros de hoy en euros futuros hay que tener en cuenta el interés compuesto, que es la tasa por la que se multiplica el valor actual para calcular el valor futuro. El interés compuesto representa el interés de un capital inicial a un tipo de interés durante un período de inversión, al final del cual los intereses obtenidos no se retiran sino que se reinvierten o añaden al capital inicial; es decir, se capitalizan.
Si se considera un solo año, el valor futuro es:
Valor futuro = Valor actual x (1 + Interés)
Si se consideran dos años:
Valor futuro = Valor actual x (1 + Interés) x (1 + Interés)
= Valor actual x (1 + Interés)2
Si se consideran n años:
Valor futuro = Valor actual x (1 + Interés)n
Hoy tenemos 1000 euros y el dinero tiene un valor del 12% anual. ¿Cuál debería ser su valor dentro de un año?
Valor futuro = Valor actual x (1 + Interés)
= 1000 x 1,12 = 1120 €
Esto significa que 1120 euros es el valor dentro de un año de 1000 euros de .
¿Cuál debería ser su valor dentro de dos años?
Valor futuro = Valor actual x (1 + Interés)n
= 1000 X (1 + 0,12)2 = 1288 €
Por lo tanto 1000 euros de hoy a un tipo de interés compuesto del 12% valdrán 1288 euros dentro de dos años.
Cálculo del valor actual de un importe futuro
El valor actual de una cantidad que haya que cobrar o pagar en el futuro es la conversión a euros de hoy de unos euros futuros. Por lo tanto, el valor actual se obtiene transformando en euros de hoy un valor futuro. Para efectuar la conversión de euros futuros en euros de hoy debemos tener en cuenta la tasa de actualización o tasa de descuento, por la que se multiplica el valor futuro para calcular el valor actual. Como su nombre indica, es una tasa que convierte (actualiza) el valor futuro en valor actual.
Si vamos a cobrar 1120 euros dentro de un año y la tasa de actualización anual es del 12%, percibiremos una cantidad cuyo valor actual es de 1000 euros. Para obtener el valor actual de 1120 euros se ha dividido dicho importe por 1 más la tasa de actualización:
Esto significa que es lo mismo cobrar 1120 euros dentro de un año que percibir 1000 euros hoy. Si queremos actualizar una cantidad que se cobrará o pagará dentro de más de un año utilizaremos la siguiente fórmula:
Obsérvese que el denominador se eleva al número de años (n) que tardará en producirse el cobro o el pago.
Si se van a cobrar 1405 euros dentro de tres años y se sabe que la tasa anual de actualización es del 12%, el valor actual será:
Por lo tanto, si el dinero vale el 12% anual, es lo mismo 1405 euros de dentro de tres años que 1000 euros de hoy.
La fórmula que se está desarrollando puede expresarse de otra forma:
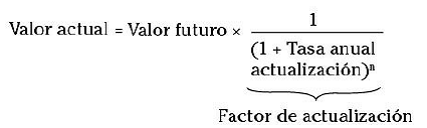
El valor actual se obtiene multiplicando el valor futuro por el factor de actualización.
Continuando con el ejemplo anterior, se haría:
Por lo tanto, el factor de actualización del ejemplo desarrollado es igual a 0,711780.
El factor de actualización puede obtenerse más fácilmente con la ayuda de tablas financieras, como la que se muestra en la tabla 16-2. Por ejemplo, el factor de actualización de un valor futuro a tres años y con una tasa de actualización del 12% es igual a 0,711780. Esto significa que 1 euro dentro de tres años con una tasa de actualización del 12% tiene un valor hoy de 0,711780 euros.
¿Cuánto vale hoy un euro que se va a cobrar dentro de treinta años si la tasa de actualización es del 30%?
La respuesta, a partir de los datos de la figura 16-2, es 0,000381 euros.
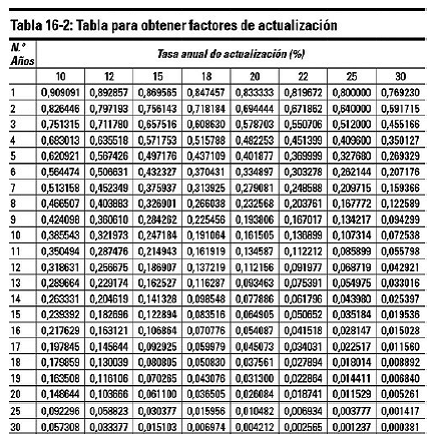
El factor de actualización es igual al valor actual de 1 euro para un número de años y para una tasa de actualización dados.
El concepto clave relacionado con la evaluación financiera y la toma de decisiones es el «valor del dinero en el tiempo». Este principio reconoce que un monto de dinero hoy no tiene el mismo valor que el mismo monto en el futuro, y viceversa. La razón principal detrás de esta diferencia de valor es la capacidad que tiene el dinero de ganar intereses o rendimientos en el tiempo.
Existen dos conceptos fundamentales asociados con el valor del dinero en el tiempo:
- Interés Compuesto:
- El interés compuesto es el proceso por el cual los intereses generados en un período se suman al capital original, y en los períodos siguientes, los intereses se calculan sobre el nuevo monto acumulado. Esto conduce a un crecimiento exponencial del valor del dinero en el tiempo.
- La fórmula para el cálculo del valor futuro (FV) con interés compuesto es: FV=PV×(1+r)t Donde:
- FV es el valor futuro.
- PV es el valor presente (o capital inicial).
- r es la tasa de interés por período.
- t es el número de períodos.
- Descuento de Flujo de Efectivo:
- El descuento de flujo de efectivo es el proceso inverso al interés compuesto. Se utiliza para calcular el valor presente de flujos de efectivo futuros, teniendo en cuenta la tasa de descuento.
- La fórmula para el cálculo del valor presente (VP) es: VP=FV(1+r)t Donde los términos tienen el mismo significado que en la fórmula de interés compuesto.